Basis Pursuit with Douglas Rachford

Test for DR algorithm for L1 minimization (BP). We do here a compressed sensing resolution (random matrix).

Add the toolbox.

addpath('../');
addpath('../toolbox/');

Dimensionality of the signal and number of measurements.

n = 200;
p = n/4;

Sensing matrix.

A = randn(p,n);

Measurements.

y = randn(p,1);

We aim at solving

min_{A*x=y} norm(x,1)

This can be rewriten as the minimization of F(x)+G(x) where F=norm(x,1) and G=i_{A*x=y} is the indicator function.

The proximity operator of the L1 norm is the soft thresholding.

ProxF = @(x,tau)perform_soft_thresholding(x, tau);

The proximity operator of the indicator of A*x=y is the orthogonal projection on A*x=y.

pA = A'*(A*A')^(-1);
ProxG = @(x,tau)x + pA*(y-A*x);

Create a function to record the values of F and the constraint at each iteration.

F = @(x)norm(x,1);
Constr = @(x)1/2*norm(y-A*x)^2;
options.report = @(x)struct('F', F(x), 'Constr', Constr(x));

Run the algorithm.

options.gamma = 5;
options.niter = 5000;
[x,R] = perform_dr(zeros(n,1), ProxF, ProxG, options);

[********************]

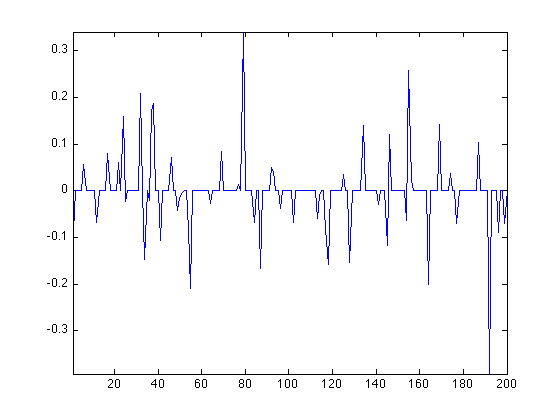
Display the solution. At convergence, it should be of sparsity p.

clf;
plot(x);
axis tight;

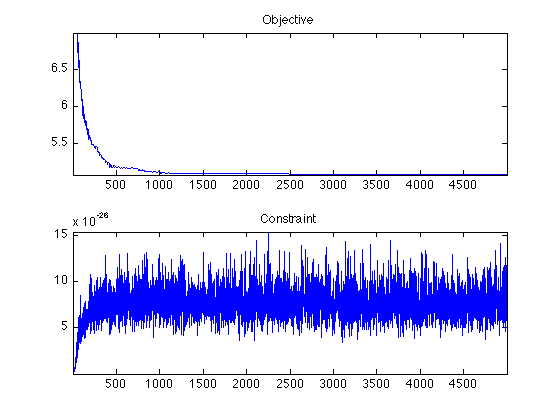
Retrieve the F and constraint function values.

f = s2v(R,'F');
constr = s2v(R,'Constr');

Display.

clf;
subplot(2,1,1);
plot(f(2:end));
axis tight; title('Objective');
subplot(2,1,2);
plot(constr(2:end));
axis tight; title('Constraint');