Total Variation Denoising

Test for Rudin-Osher-Fatemi denoising (ROF) using FB-like method.

addpath('../');
addpath('../toolbox/');

Load image.

n = 256;
y = load_image('lena',n*2);
y = rescale(crop(y,n));
y = y + randn(n)*.06;

Display it.

clf;
imageplot(clamp(y));

We aim at minimising:

min_x 1/2*norm(y-x,'fro')^2 + lambda*norm(K(x),1)

Regularization parameter.

lambda = .2;

where K is a vectorial gradient and norm(u,1) is a vectorial L1 norme.

K = @(x)grad(x);
KS = @(x)-div(x);

It can be put as the minimization of F(K*x) + G(x)

Amplitude = @(u)sqrt(sum(u.^2,3));
F = @(u)lambda*sum(sum(Amplitude(u)));
G = @(x)1/2*norm(y-x,'fro')^2;

The proximity operator of F is the vectorial soft thresholding.

Normalize = @(u)u./repmat( max(Amplitude(u),1e-10), [1 1 2] );
ProxF = @(u,tau)repmat( perform_soft_thresholding(Amplitude(u),lambda*tau), [1 1 2]).*Normalize(u);
ProxFS = compute_dual_prox(ProxF);

The proximity operator of G.

ProxG = @(x,tau)(x+tau*y)/(1+tau);

Function to record progression of the functional.

options.report = @(x)G(x) + F(K(x));

Run the ADMM algorihtm.

options.niter = 300;
[xAdmm,EAdmm] = perform_admm(y, K,  KS, ProxFS, ProxG, options);

[********************]

Display image.

clf;
imageplot(xAdmm);

Since the functional to mimize is stricly convex, we can use a FB scheme on the dual problem.

GradGS = @(x)x+y;
L = 8;
options.method = 'fista';
[xFista,EFista] = perform_fb_strongly(y, K, KS, GradGS, ProxFS, L, options);

[********************]

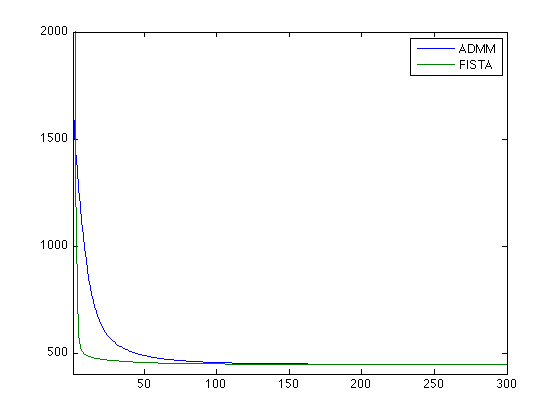
Compare the energy decays.

clf;
plot([EAdmm(:) EFista(:)]);
axis tight;
legend('ADMM', 'FISTA');
axis([1 length(EAdmm) EFista(end)*.9 2000]);